확률에 대해 기본적인 개념을 한가지 간단한 에피소드를 통해 이해를 해보자.
압정을 던져 머리(Head) / 꼬리(Tail)를 베팅하는 도박이 있다고해보자.

압정은 던져서 나온 결과가 쉽게 50대50이라 판정할수 없다. ( 모양이 균일하지 않기 때문에)
부자가 압정을 던져서 나온 결과를 잘 분석해보자고 나한테 제안하였다고 해보자.
부자가 "어떻게 하면 내가 돈을 딸수 있을까? "라고 물어보았다.
나는 우선 "몇번던져보세요~" 라고하였다.
부자는 5번정도 압정을 던졌다.
머리(Head) 2번 , 꼬리 (Tail)이 3번 나왔다.
위의 결과를 토대로 꼬리(Tail)이 더 많이 나왔으니 꼬리(Tail)에 배팅하세요라고 말할수 있을까?
왜 Tail은 3/5 , Head 는 2/5라는 결과가 나왔을까??
위의 물음에 대한 답을 알려면 확률에 대한 지식이 필요하다.
우선 위의 실험을 Binomial Distribution 이라는 확률분포를 통해 계산해보자.
Binomial Distribution 은 확률분포가 continous 가 아니다. 그리고 Discrete probability distribution 이다.
(Discrete라는 의미는 결과가 True / False로만 나타낸다는 의미로 알고 있으면 된다.)
압정 던지는 각각의 시행( Event)는 서로독립이다. (각각 Event 가 서로의 결과에 영향을 주지않는다는 의미이다.)
그러면 이제 압정던지는 Event 를 확률로 표현해보자.
P(H) : 압정을 던졌을때 Head가 나올 확률을 의미한다.
P(T) : 압정을 던졌을때 Tail이 나올 확률을 의미한다.
P(H) = Θ , P(T) = 1 - Θ
부자가 압정을 5번 던졌는데 아래와 같이 나왔다.
Head , Head , Tail , Head , Tail
이것을 확률로 표현하면 아래와 같다.

위에서나온 H,H,T,H,T를 Data라 하고 D라고 표현해보자.
P(D|Θ) : Θ라는 확률정보가 주어졌을때 D라고하는 데이터가 관측될 확률이라 정의해보자.
그러면 아래와 같이 표현할수 있다.

이제 Maximum 확률 Θ에 대해 구해보자.
여기서 우리는 한가지 아래와 같은 가정이 필요하다.
압정 던지는의 도박결과는 Θ의 Binomial Distribution 을 따른다고 가정하자.
어떻게 하면 우리의 가정이 강해질까? 그래서 가정이 참이다라고 말할수 있을까?
Θ를 최적화해서 가정을 강하게 만들어 볼수 있다.
어떤 Θ를 선택을했을경우에 데이터를 잘설명할수 있을까? 이것을 찾아내는것이 확률의 요체이다.
첫번째로 알아볼것은 MLE이다.
관측된데이터의 등장할 확률을 최대화하는 Θ를 찾아내는것이다.
그 Θ를

(Θ Hat이라한다.)
부자의 압정 던지는 결과에 MLE를 적용해보자

로그를 취해도 P가 최대화 되는점은 동일하다.
(곱을 더하기로 바꿀수 있다. 지수가 앞으로 나올수 있다라는 장점이 있다.)
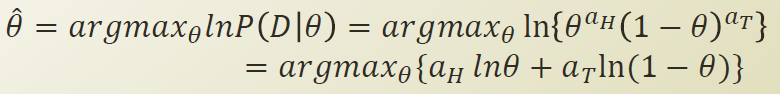
위의함수를 미분해서 최대값 Θ을 구할수 있다.

즉 압정을 던져진 횟수 분에 나온횟수가 최대값 Θ 가 된다.
MLE 관점에서 본 최적화된 Θ hat 이 나오게된다.
위의 결과를 부자한테 말하면된다.
""압정의 Head가 나올확률은 MLE를 통해 3/5가 이렇게 나왔다.~""
부자는
"그래 좋다. 너가 위의 확률을 계산하는동안 좀더 던져봤어.
50번을 더 던졌는데 H : 30 / T: 20가 나왔어..
5번중에 3번이나 50번중에 30번이나 동일한것이냐??
위와 같이 물었다. 정말 두가지 결과는같다고 말할수 있냐? 부자가 많이 던진것은 헛수고한겁니다라고 말할수 있을까?
우리는 아래와 같이 대답해야한다.
여러번 더 던지면 우리가 말한 결과는 Θ hat이지 Θ를 말한것이 아니다.
즉 파라미터를 추론한것이지 파라미터가 이것이다라고 말한것은 아니다.
True parameter Θ* 는 에러가 없이 압정을 던졌을떄 나오는 결과이다.
즉 Θhat과 Θ*는 동일할수 없다.
통계관점에서 아래의 수식이 있다.

N : Trial 값 ( 압정을 던진 시행횟수)
ε : 에러
위의식은
1)error bound가 커진다면 에러가 발생할 확률은 작아진다는 의미.
2)N이 커지면 에러가 발생할 확률은 작아진다.
실제 Θ와 Θ hat이 0.1차이 (우리는 0.6이라주장)가 나면서 0.01%보다 작게 만들수 있냐?
에러를 0.1이하로 하려면 어떻게해야하나?
위의 수식의 의미를 통해 알아낸것 처럼
"압정을많이 던지면됩니다.~~라고말하면된다. 그래서 Θ hat을구하면됩니다.~~" 라고말하면 된다.
위의 과정을 PAC라한다
P : 아마도 실제 Θ와 Θ hat가 ε보다 클 확률 범위내에서는
A : 오차범위내에서는
C : Correct한 러닝의 결과물이 Θ hat이다.
이것이 PAC러닝의 결과물이다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 1.4 Probability and Distribution (0) | 2019.05.29 |
|---|---|
| Week 1.3 MAP (0) | 2019.05.27 |
| Week 7.8 Potential Function and Clique Graph (0) | 2019.04.22 |
| Week 7.7 Variable Elimination (0) | 2019.04.19 |
| Week 7.6 Inference Question on Bayesian network (0) | 2019.04.17 |
