1.2강의를 통해 MLE 관점에 대하여 설명하였다.
1.2 강의 MLE 링크 : https://deadsquart.tistory.com/18
Week 1.2 MLE
확률에 대해 기본적인 개념을 한가지 간단한 에피소드를 통해 이해를 해보자. 압정을 던져 머리(Head) / 꼬리(Tail)를 베팅하는 도박이 있다고해보자. 압정은 던져서 나온 결과가 쉽게 50대50이라 판정할수 없다...
deadsquart.tistory.com
그런데 베이즈라는 사람이 부자에게
"압정을 던지면 정말 60%의 확률로 Head가 나올거 같냐???
Head / Tail 이 나올확률이 50대 50이라고 생각안하세요??
라고 되물었다.
부자는 아래와 같이 대답하였다.
"나도 처음에는 50대 50의 확률이 나올것 같다고 생각했는데 , 막상 던져보니깐 60%가 나오더라.."
베이즈는 아래와 같이 말하였다.
" "압정의 Head 와 Tail 이 50대50의 확률로 나온다"라는 사전정보를 Parameter 추정과정에 넣을수 있습니다.
사전정보를 내포하고 있는P(Θ)에 대해 한번 알아보죠.
제가 Θ를 알아내는 중요한 공식을 알아냈습니다. 아래와 같이 정리할수 있습니다. !! "

1) P(D) : 데이터가 관측될 확률 - 중요하지 않다. 이미 주어진 사실이기 때문에 우리가 어떻게 할수 없다. 그래서 Normalizing Constant 로 생각한다.
2) P(Θ) : 사전 정보 - 압정의 Head 와 Tail 이 50대50의 확률로 나온다라는 생각
(Latent 한 Drive force 이기 때문에 중요)
3) P(D|Θ) : Θ가 주어졌을때 데이터를 관측할 Likelihood
4) P(Θ|D) : 데이터가 주어졌을때 Θ의 확률
베이즈는 또다시 말하였다.
"P(D|Θ)는 이미 MLE를 구하면서 알아냈으니, (Binomial Distribution 에서 나옴.)
P(Θ)를 추가하기만 하면 P(Θ|D)를 구할수 있습니다.
Beta distribution을 이용해서 P(Θ)를 구하면될거 같아요. !!! "
Beta distribution 란 특정 범위내에서 0에서 1로 Comfine 되어있는 C.D.F. (Cumulative Distribution Function) 이다.
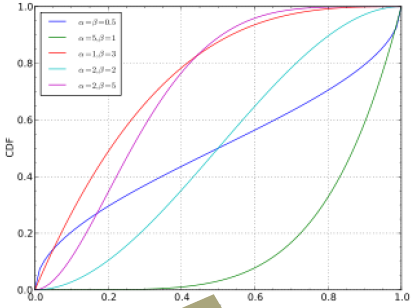
0에서 1의 값을 가지는 Probability 성격을 표현하고있다.
Beta distribution 을 식으로 표현하면 아래와 같다.

위의 [1.베이즈 공식]에서 우항의 분모인P(D)는 위에서 말한것처럼 Normalizing Constant 취급할수 있기 때문에 위의식은 아래와 같이 비례식으로 표현할수 있다.
P(Θ|D)는 Binomial Distribution 에서 구할수 있고 , P(Θ)는 위의 [2.Beta Distribution]을 통해 정리할수 있다. 이것을 아래의 비례식에 대입 및 정리해보면
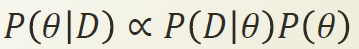
아래와 같이 정리된다.

MLE을 통해 서는 P(D|Θ)를 이용해 Θ hat 구할수 있는데 ,
MAP는 P(Θ|D)를 이용해 Θ hat 를 구하게 된다. 극점을 이용한 최적화 하면 아래와 같이 나온다.

위의 식을 이용하면 사전 정보를 넣어 Θhat을 조절할수 있다.
위의 식을 통해 시행횟수를 많이하면 알파와 베타에 의한 영향력이 줄어든다.
그러면 MLE 와 MAP 를 통해 구해진 Θ hat 값이 같아진다.
하지만 알파 h / 알파 t 가 작으면 사전정보는 중요한 역할을 한다. (관측값이 작은경우)
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week2.1. Rule Based Machine Learning Overview (0) | 2019.06.11 |
|---|---|
| Week 1.4 Probability and Distribution (0) | 2019.05.29 |
| Week 1.2 MLE (0) | 2019.05.24 |
| Week 7.8 Potential Function and Clique Graph (0) | 2019.04.22 |
| Week 7.7 Variable Elimination (0) | 2019.04.19 |
