1. Marginalization and Elimination
Partial joint 를 구할때는 Full joint 의 형태로 변경해서 marinalization 하면 구할수 있다.


알람이 울리고, 도둑이침입하고, Mary가 전화할 확률을 구해보자. ( P(A= true, B= true, MC = true) = ? )
구하고자 하는것은 Parial joint 확률인데 , Full joint 확률을 통해 구할수 있다.

식에는 아무런 문제가 없지만 , 시그마를 E에대해서 한번 Loop를 돌리고, JC에 대한 시그마 Loop를 돌리기 때문에 계산복잡도가 늘어난다.

시그마를 위의 식처럼 이동시키면 , 이중 Loop를 돌리지 않기 때문에 계산복잡도가 이전 식에 비에 단순해질수 있다.
P(b) , P(mc|a) 는 JC 나 E에 영햐을 받지 않기 때문에 시그마 밖으로 뺼수 있다.
2. Variable Elimination
John 이 전화하고 , Mary 가 전화했을때 지진이 일어날 확률을 구해보자.
( P ( e | jc, mc ) = ?? )
P ( e | jc, mc ) = α P (e,jc,mc)
α = 1 / P(jc,mc)
위의 Partial joint를 full joint로 변환해보자.
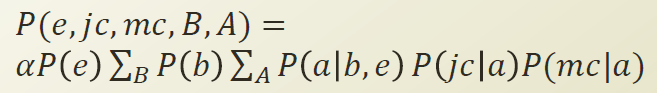
여기서 각각의 확률들은 continous 값을 내보내고 있다. (위의 Table 참조. 예를 들어 알람이 울렸을때 John 이 전화할 확률은 0.9이다. ) 즉 확률들을 Function으로 생각할수 있다. 그래서 위의 식에서 확률을 Function으로 변경해보자.

변경한 식은 좀더 곱셉을 통해 간단히 나타낼수 있다.

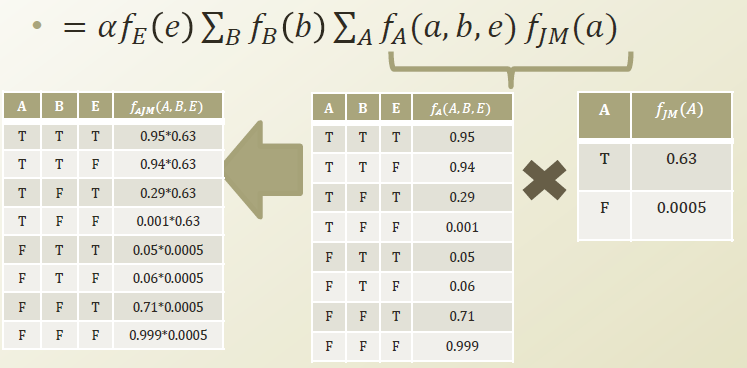
이런 식으로반복하다보면 아래와 같이 간단히 변경된다.

'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 1.2 MLE (0) | 2019.05.24 |
|---|---|
| Week 7.8 Potential Function and Clique Graph (0) | 2019.04.22 |
| Week 7.6 Inference Question on Bayesian network (0) | 2019.04.17 |
| Week 7.5 Factorization of Bayesian networks (0) | 2019.04.16 |
| Week 7.4 Bayes Ball Algorithm (베이즈볼) (0) | 2019.04.14 |
