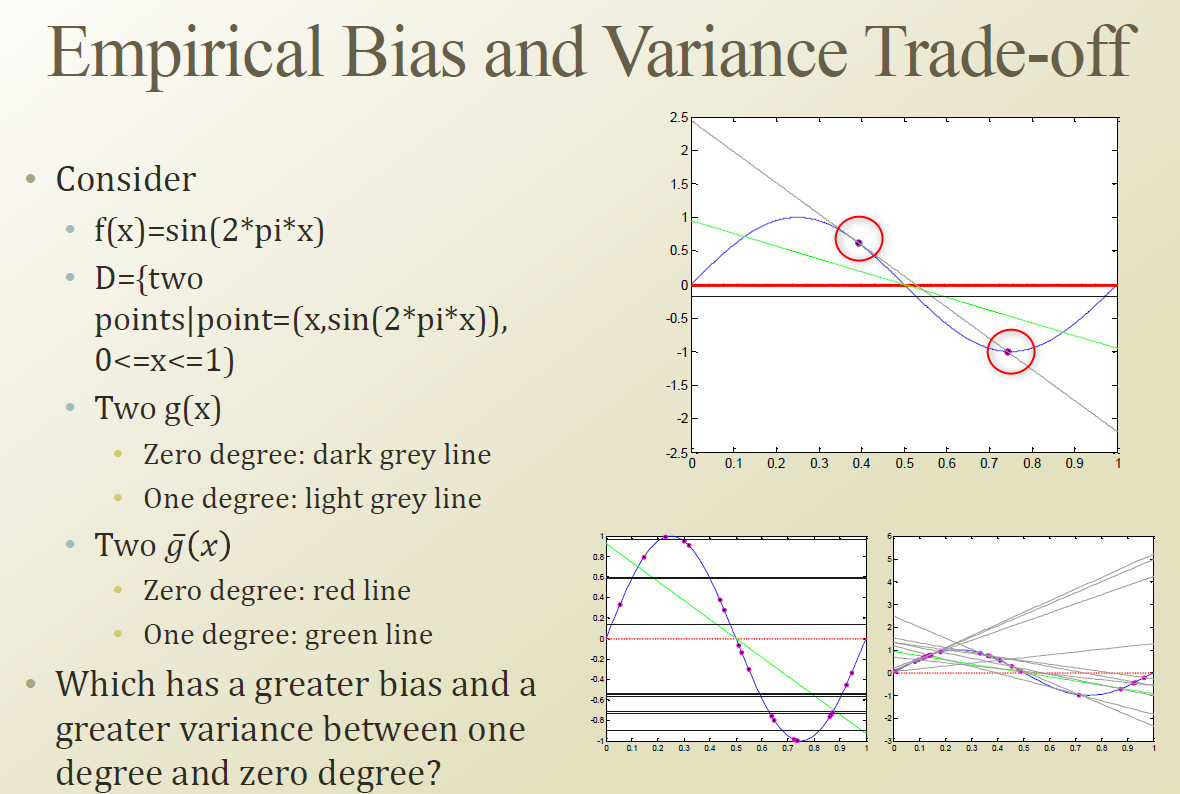
위의 Sine 함수가 있고 , 현실에서 일어날수 있는 True function 이라 해보자. [가정]
True function을 모르는 상태에서 true function 을 approximation 하는것인데 , 에러에 대해 분석을 해야하기 때문에 실제 true function 이 " sine 함수 이다." 라고 가정을하고 진행을 해보자.
true function 중에서 우리가 관측할수 있는것은 몇개의 point 밖에 없다.
위의 그래프에서 2개의 보라색 점이 관측되었다고 해보자. (빨간색 원)
그러면 아래와 추정 할수 있다.
1) 검은색 선에서 에러가 있으면서 관측된점이다.
2) 회색선 (1차함수)에서 발생한것이다. ( 에러가 없다.)
하지만 위의 2가지 모두 틀리다는것은 우리는 알수 있다.
우리가 Sin 함수 전체를 다 알고 있는 상태에서는 만약 1차함수로만 approximation 해야한다면 어떤것이 더 맞다고 할수 있을까? 결론부터 말하면 위의 그림에서는 녹색 선이 가장 best fitting 이라 할수 있다.

sampling 이 위 왼쪽그래프의 빨간색 원의 두점으로 되었다고 생각해보자. 그러면 일차식이 상향하는 방향으로 가야되는데 , 위의 회색선을 적용하면 다른점에 대해서는 에러가 더 커질수 있다.
즉 좋은 결과가 나올수 있지만 위험한 결과도 나올수 있다.
그리고 constant 선(검은색선)에 대해서는 위의 회색선처럼 크게 벗어나는 에러가 발생하지는 않지만 , 성능이 떨어지는 단점이 있다.
즉 회색선과 검은색선은 trade off 관계라 할수 있다.
물론 Complex 한 모델이 좋을수 있지만 ( 회색선) , 우리가 가진 sampling 데이터의 한계 때문에 위험을 감수하고 Complex한 모델을 선택할수 있을지는 의문이다.

위의 각각 두 그래프는 average hypothesis 가 생성되었다.
현실에서는 Bias 와 variance를 구할수 없다. True function 을 모르기때문이다. 하지만 여기서는 true function을 sine 함수로 가정하였기 때문에 Bias 와 variance를 구할수 있다.
Occam's Razor
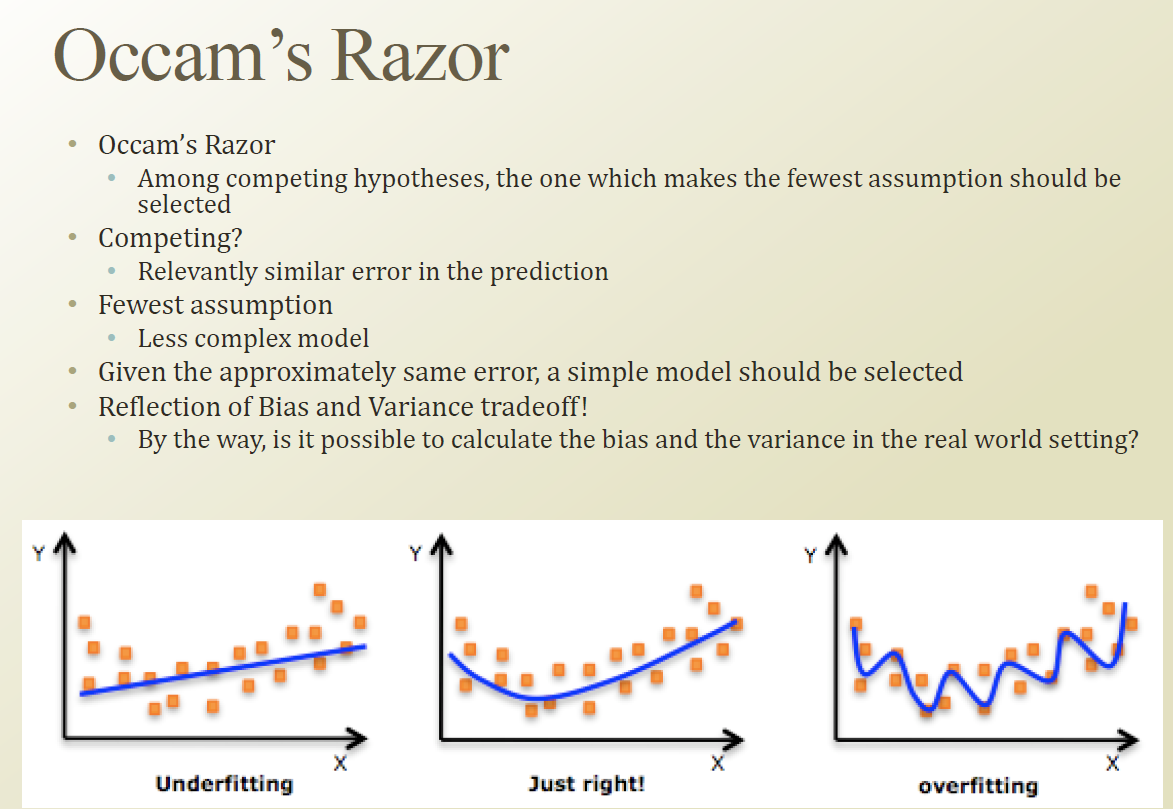
Occam's Razor 는 여러개의 competing 한 hypotheses가 있을 경우에는 , simple 한 hypothesis가 낫다라는것이다.
즉 에러가 비슷하면 simple 모델이 낫다라는 의미이다.
bias와 variance 의 trade off 관계를 잘 반영해서 에러가 동일하다면 stable 한 모델이 선호된다는 의미이다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 6.5. Performance Metrics (0) | 2019.08.18 |
|---|---|
| Weeek 6.4 Cross Validation (0) | 2019.08.17 |
| Week 6.2. Bias and Variance (0) | 2019.08.10 |
| Week 6.1. Over-fitting and Under-fitting (0) | 2019.08.09 |
| Week 5.9. SVM with Kernel (0) | 2019.08.07 |
