Dual SVM with Kernel Trick
이전시간에 배운 w를 바로 직접적으로 계산한것이 Primal Problem 이고
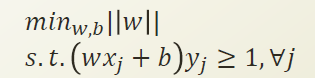
Dual problem 으로 바꾸면서 w를 α로 Learning 하는것으로 바뀌었다.
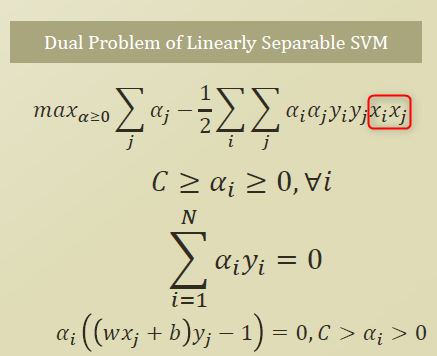
Dual problem 에서의 xi, xj 가 φ를 넣어가지고 다른차원으로 넘겨서 내적을 하겠다는것으로 변경할수 있다.
(아래 식 참고)
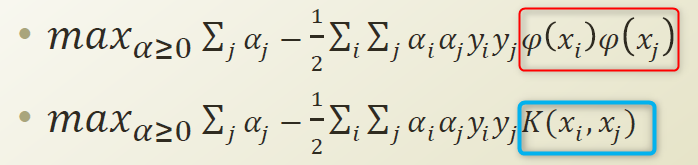
φ를 정의를해서 x를 넘겨버린 차원으로 SVM을 돌리자는것이 아니라 내적을 하는 형태이기때문에 φ부분만 Kernel로 대체하자는 것이다.
Kernel로 대체를 하면 K(xi,xj)의 Kernel값(K)만 앞에다가 계산하는 형태가 된다. xi , xj는 이미 우리가 알고있는 input값이라 K도 구할수 있고 Constant term이 되버린다.
식을 정리해 보면 , w와 b를 아래와 같이 정리가 된다.
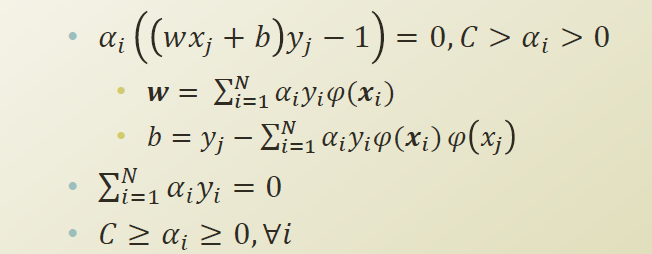
w라는 DB의 방향성에 대해서는 Kenel 형태로 전환이 안되고 여전히 φ로 차원 mapping function으로 되어 있다.
b는 φ(xi)φsj) 형태이기 때문에 kernel로 변경이 된다.
w와 b가 필요한 이유는 w,와 b를 활용해 Classification을 하기위함이다.
예를 들어 x를 넣어 양수가 되면 positive case가 되고, x를 넣어 음수가 되면 negative case가 되는 것이다.
DB를 그리려는 목적이 아니라 DB를 이용해 임의의 인스턴스가 주어졌을때 이것이 Positive / negative 인지 알아내려는것이 목적이다. 그래서 w 자체를 알려고 노력하지 말고 , 인스턴스가 주어 질때 결과값만 알아내보자는 식으로 생각을 하도록 하자.

Kernel을 이용하면 w를 앞으로 올 feature(예측값)에 대해서도 다른 차원으로 보내야 한다.
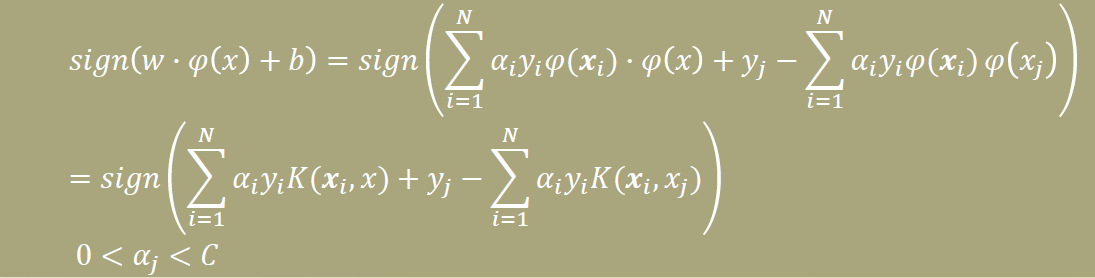
위의 sign (w * φ(x)+b) 의 형태에 아래를 대입해 보면 w가 있는 항도 Kernel의 형태로 변하게 된다.
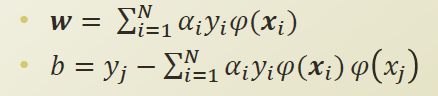
α는 quadratic programing을 통해 알수있고 , y는 Dataset을 통해 알수 있다.
즉 w 값을 찾아내기는 불가능하지만 , 여전히 classification은 가능하다는 결론을 내릴수 있다.
SVM은 Hard margin은 현실데이터에서는 잘 존재하지 않았다. Error case에 대해서는 infeasible한 내용이다라고 판단하였다.
그것을 보안하기위해 Soft margin을 추가해 error에 대해 penalty를 주었다.
만약 진실로 non-linear한 behavior를 보이면 적용하기 어려웠다.
Non-linear하게 만들기위해서 linear model을 높은차원에 있는 데이터에 적용하는 형태로 만든것이다. 근데 Kernel trick을 이용하면 높은차원으로의 데이터 transform을 쉽게할수 있었다.
여기까지하면 SVM을 이용해서 non-linear한 DB도 만들수 있고, DB를 넘는것에 대해서는 penalty 를 줄수 도 있다. 즉 classification을 쉽게할 수 있는 기반이 만들어 졌다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 6.2. Bias and Variance (0) | 2019.08.10 |
|---|---|
| Week 6.1. Over-fitting and Under-fitting (0) | 2019.08.09 |
| Week 5.8. Kernel (0) | 2019.08.06 |
| Week 5.7. Primal and Dual with KKT Condition (0) | 2019.07.20 |
| Week 5.6. Rethinking of SVM (0) | 2019.07.20 |
