Mapping Functions

위의 (a) 그림은 a,d 는 false , b,c 는 true 라 하고 Linearly separable 하지 않다.
2차로 뻥튀기 시키고 (Mapping) 원래 a,b,c,d,의 값을 대입해보면 (b)와 같이 그려지게 된다. (3차원)
그리고 특정 DB를 만들수 있게 된다.
Feature space에서 interaction 을 많이 만들어서 linearly separable 하지 않는 case를 linearly separable 하게 만들어서
linear claasifier를 적용해서 이게 마치 Non-linear classifier인것처럼 행동하게 끔 만들어주는 방법이 있다.
하지만 interaction을 더하는것은 좋은방법이 아니다. 왜냐면 feature space가 늘어나게된다. 그러면 컨트롤하기 힘들다.
그러면 어덯게 하면 Mapping function을 smart하게 잘 사용 할 수 있을까? 그래서 Kernel이라는 아이디어가 나오게 된다.
Kernel

Kernel은 두백터의 다른 space 상의 inner product (내적) 형태로 만들어보려한다. φ(푸사이) 로 Xj 와 Xi 두점을 다른 차원으로 보내린 상황에서의 내적을 Kernel로 정의한다.
Kernel은 아래와 같이 여러가지 종류가 있다.
- Polynomial(homogeneous)
- Polynomial(inhomogeneous)
- Gaussian kernel function, a.k.a. Radial Basis Function
- Hyperbolic tangent, a.k.a. Sigmoid Function
Polynomial Kernel Funciton

x, z 의 2개의 점이 있다고 생각해보자.
Polynomial Kernel Function of degree 1 은 아무런 차원을 이동하지 않은 있는 그대로의 내적이다.
Polynomial Kernel Function of degree 2 는 차원을 3개로 늘려 내적을 한다.
이것을 쭉 차원을 높이다 보니 아래와 같은 규칙이 보이게 된다.
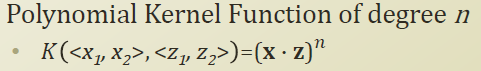
위의 Polynomial Kernel Function of degree 2를 보면 x,z의 2차원 point를 3차로 보내서 내적을 하는것나 , x,z를 먼저 내적해서 3차로 보낸것이 동일하다는 특징을 보인다.
즉 정리를 해보면 , Kernel의 개념은 내적을 먼저 하고 다른차원으로 보내버리는것이고 , 이것은 계산함에 있어서 , feature 수가 크게 증가하지 않기 때문에 계산적인 측면에 있어서 매우 효율적이다.
그러면 높은 차원의 정보를 쉽게 다룰수 있게된다. 그래서 이것을 이용해서 infinite 차원의 내용을 표현해 보겠다는것이
Kernel trick 이다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 6.1. Over-fitting and Under-fitting (0) | 2019.08.09 |
|---|---|
| Week 5.9. SVM with Kernel (0) | 2019.08.07 |
| Week 5.7. Primal and Dual with KKT Condition (0) | 2019.07.20 |
| Week 5.6. Rethinking of SVM (0) | 2019.07.20 |
| Week 5.5. Soft Margin with SVM (0) | 2019.07.19 |
