Rejection sampling을 보완하기 위해 만든것이 Importance sampling 이다.
Sampling을 왜하냐? Expectation 을 계산하거나 , 확률값을 계산하기 위해 Sampling을 한다.
즉 , 위의 2가지만 잘할수 있으면 sampling을 무식하게 여러번하지 않아도된다. 그래서 도입된것인 Importance sampling 이다.

특정 함수에 대한 E(f)를 구해보자. f에 들어가는 random variable (z)이 있고, random variable을 generate 하는 확률분포 p(z)가 있을수 있다.

위의 식의 제일 우항은 non equal 이다. 왜냐면 제일 우항을 제외하고는 무한대에 대한 확률을 다 계산하는것으로 나타내지만 현실은 불가능하다. 현실은 개별 Instance를 samping 하고 개별 인스턴스의 발생 확률을 구할수 있다.
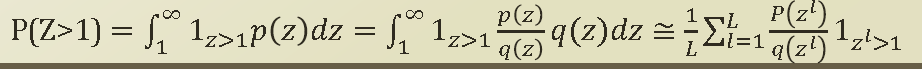
특정 sample 이 1이상인 확률을 구한다고 해보자. => P(Z>1)
P(z)가 1 이상인 case를 모두 summation 하면된다. 이것을 directly 계산이 쉽지않다. ( 적분이 쉽지않다. ) 그래서 sampling을 이용한다. q(z)의 sampling distribution을 활용하여 개별 q(z)을 이용해서 sampling을 여러번한다.
sampling의 하나하나 instance가 zl 이다. f는 1z>1 의 identity 함수이고, q는 zl을 활용했던 sampling distribution 값이고 , p(zl)은 sampling을 직접하지 않아도, probability evaluation 할수 있다는 가정 때문에 계산할수 있다. 뒤의 zl>1 부분은 1보다 크면 1 , 1보다 작으면 0으로 판단한다. 이렇게 sample을 통해 해결하게되는 과정을 importance sampling 이라 한다.
그러면 importance sampling을 discrte 한 domain 에서는 어떻게 하는지 알아보자.

sampling weight를 1로 두고 시작한다. coin toss를 통해 sampling을 하나하나 해 나간다.
0.001의 확률로 T가 나오는데 , 0.999의 확률로 F가 나왔다고 해보자. 여기서 sampling weight를 잡아준다. 지금까지의 확률이 얼마큼 important 하게 발생하느냐에 따라 weight를 잡아준다.
여기서 NormSW 는 앞의 numerical view의 1/L*q(zl)이라 볼수 있고, SumSW 는 p(zl) 로 볼수 있다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 10.5 Markov Chain for Sampling (0) | 2019.12.10 |
|---|---|
| Week 10.4 Markov Chain (0) | 2019.12.02 |
| Week 10.2 Rejection Sampling (0) | 2019.11.27 |
| Week 10.1 Forward Sampling (0) | 2019.11.13 |
| Week 9.5 Baum-Welch Algorithm (0) | 2019.11.05 |
