약간의 조건을 가지고 샘플링하는것.
샘플링을 여러번 해야한다. (iteration 을 여러번 해야한다.)
우선 rejection sampling을 discrete 관점에서 알아보자.
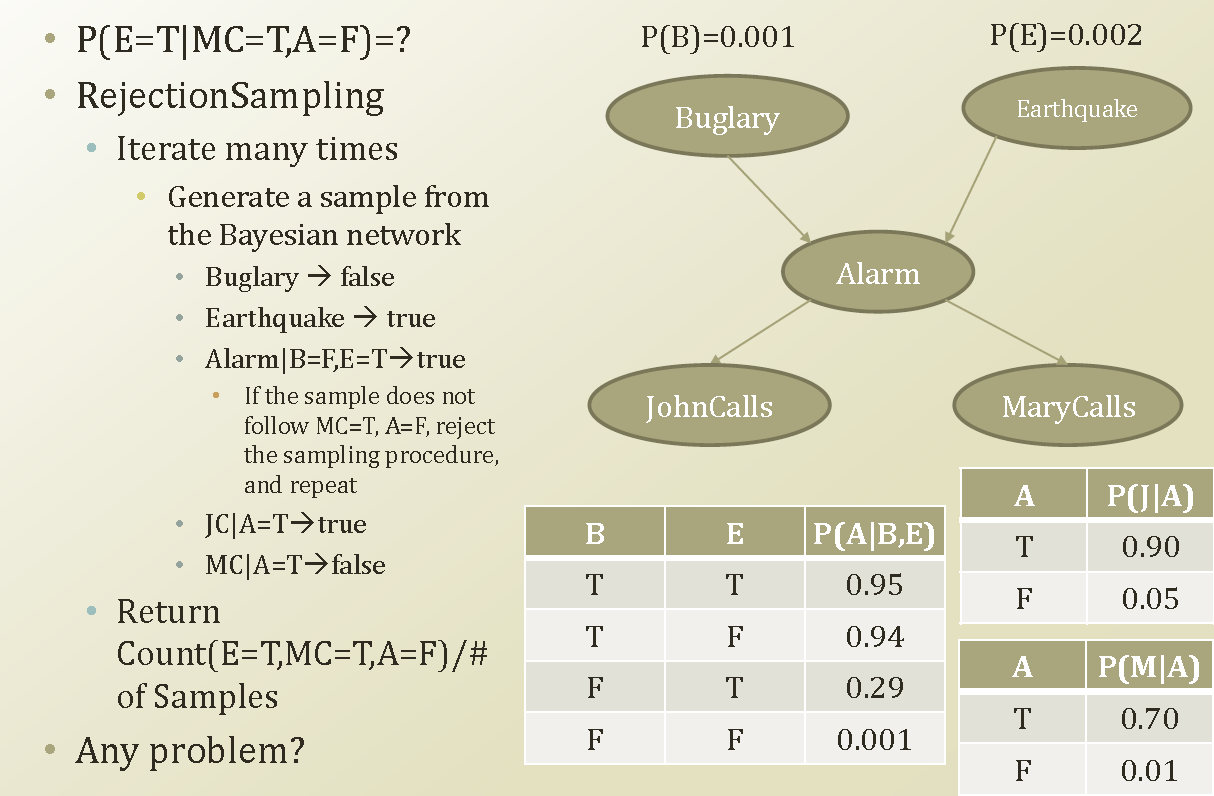
Forwad sampling과 유사한 방식으로 유사하게 흘러간다.
위에서 P(E=T|MC=T, A=F)를 구하는 과정에서 Alarm|B=F,E=T 라는 샘플링은 A=F 라는 given 에 맞지 않다.
그러면 Alarm|B=F,E=T 이 sample은 쓸수 없게 된다. 즉 이 sample은 reject 하겠다. 그래서 reject sampling 이라한다.
Rejection sampling을 수치적 관점에서 알아보자.
아래그림에서 p(x)는 우리가 sampling하고 싶은 확률분포이다. 우리가 잘 알고 있는 특정 distribution 에서 샘플링한다고 해보자.
q(x)가 Normal 분포를 따른다고 해보자, 그리고 p(x)는 mixture distribution 이라해보자. p(x)를 감쌀수 있는 sampling distribution 을 만들어보자.

우리가 알아보려는 p(x)는 summation 하면 1이라는 제약조건을 가지고 있다. 그래서 높이가 한정되어 있다.
그래서 이 최대 높이를 뛰어넘는 M을 곱해 distribution을 만들수 있다.
normal distribution을 따르는 값을 하나 sampling 을 해볼수 있다. 그포인트를 xi라는 지점이었다고 해보자.
이제 xi 라는 지점에서 이 sample을 받아 들일것인지 안 받아들인것인지 결정할수 있다.
p(x)의 parameter 들은 우리가 알수 없지만 , evaluate는 할수 있다. 위 그림의 높이는 쉽게 알수 있다. (Xi ~A 의 높이)
Normal Distribution 의 M을 곱한 값의 높이로 나누어 그 확률만큼을 가지고 sample을 accept 할것인지 reject 할것인지 결정하겠다는 것이 numerical view에서의 reject sampling 이다. 위의 Rejection Region 이 Rejection 이 될것이다.
M이 P(x)를 envelope 하지 않으면 Rejection sampling이 작동하지 않는다. 즉 M이 커져야한다. M이 커지면 Rejection 되는 region이 커진다. 그래서 sampling하는 시간상의 단점이 발생하게 된다.
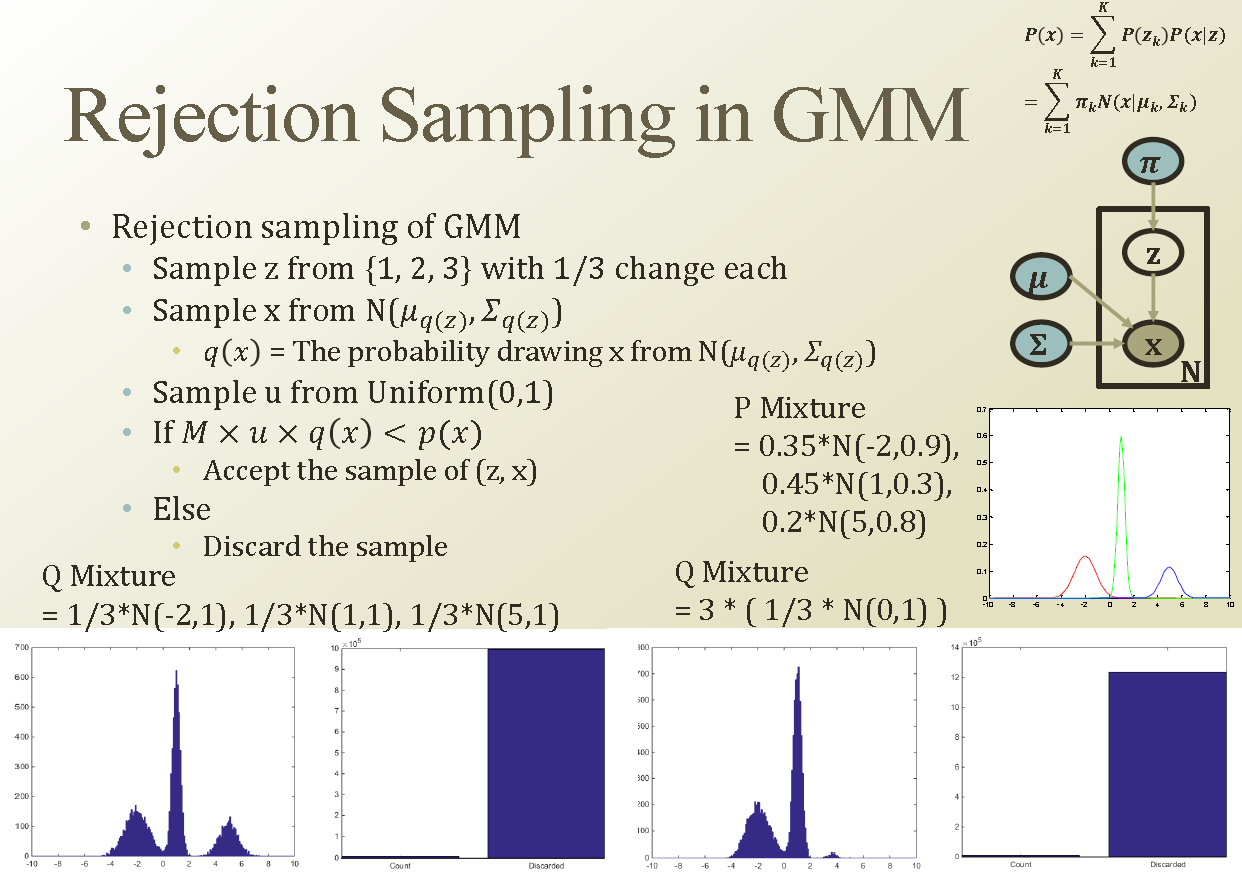
위의 왼쪽그림은 sampling을 NOrmal에서 M을 1/3을 주고, Mixture 된 상태에서 sampling 한경우이다.
위의 오른쪽그림은 sampling을 하나의 Normal에서 M을 3을 주고 sampling을 한 경우이다.
오른쪽 그림의 제일 오른쪽 봉우리는 작은데 이것은 envelope가 잘되지 않은 경우이다. (Under sampling 된경우이다.)
Rejection sampling도 여전히 계산 속도의 문제가 발생한다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 10.4 Markov Chain (0) | 2019.12.02 |
|---|---|
| Week 10.3 Importance Sampling (0) | 2019.11.28 |
| Week 10.1 Forward Sampling (0) | 2019.11.13 |
| Week 9.5 Baum-Welch Algorithm (0) | 2019.11.05 |
| Week 9.4 Viterbi Decoding Algorithm (0) | 2019.11.04 |
