Decoding 중 Viterbi Decoding 알고리즘이 많이 쓰인다.
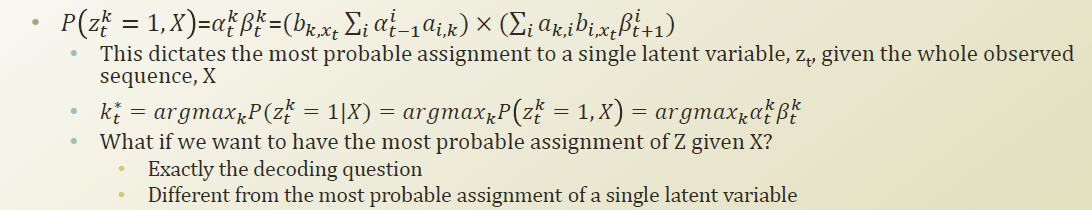
Forwad probability 와 Backward probablity는 특정 time t에서 latent fator가 특정 k 클러스터에 속할 joint 확률을 구하기 위해 Forwad probability 와 Backward probablity의 곱으로 나타낸다.
이 구조는 재귀적 구조로 나타내진다. 이렇게 되면 특정 time t 의 latent variable에 대한 joint 가 된다는것이다. 이것은 conditional probability도 가능하다는 말이다. x가 given 일때 특정 time t의 latent variable에 대해서는 가장 most probable 한 assignment 를 할수 있겠다라는 내용이다.
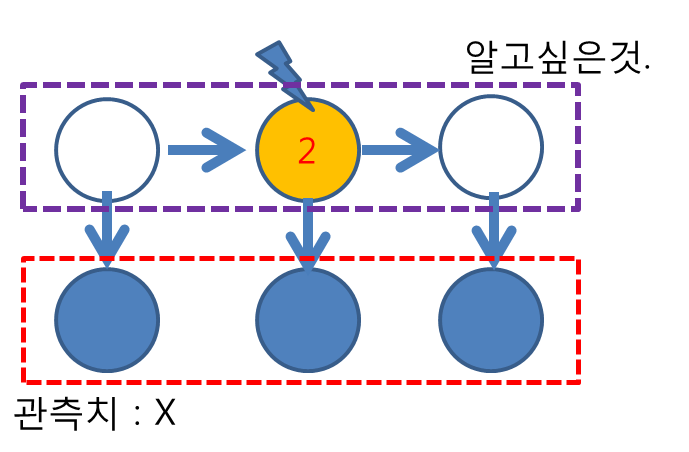
이것의 문제점은 single latent variable에 대한 assignment 라는 것이다. whole sequence를 보고 whole sequence에 대한 latent variable에 대해서 assign 하고 싶은데, 이것을 decoding question 이라 한다. 즉 위의 그림에서 관측치 X를 알면 ( 빨간네모) , 2번의 노란색을 알수 있다. 그런데 알고싶은것은 보라색 네모의 전체 sequence (Z)이다. 이것을 decoding question 이라한다.
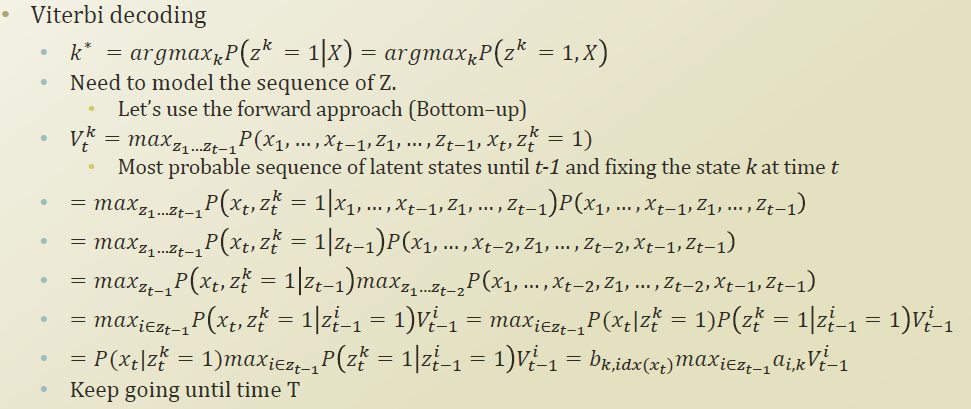
K * : most probable assignment of 특정 클러스터 K, X라고 하는 전체 sequence가 given 인 상황에서 확률을 max인 상황을 한번 assignment 해보자라는것.
Vt k : x에 대해서 t-1 time 까지 (이전 time )의 whole sequence(x1,....xt-1 + z1,....zt-1) 와 지금 estimation 하려는 latent factor가 어떤 클러스터에 속하는냐(zkt=1)와 지금 관측되고 있는 정보(xt)가 관측될 확률을 maximize 하는 형태로 z1에서 zt-1 을 바꿔보겠다는 의미
Viterbi 알고리즘도 repeating 구조이기 때문에 Dynamic program을 적용하여 전체 whole sequence 에 대한 most probable assignment를 얻게 된다.
Dynamic program의 예시를 살펴보자.
아래는 자동차공장의 조립라인이다.

각각원에 적힌것은 그 station에서의 소요시간이다. 화살표는 현재 station에서 그 다음 station으로 가는 경로를 나타낸다.
어떤 station에서 조립하는것이 시간이 가장 적게 걸릴것인가라는 계산에 dynamic programming 이 사용된다.
우리가 구하려는 most probable assignment를 찾는것과 유사한 형태이다.

위의 예실르 확률의 관점에서 다시한번 보자.

Vt k 는 [Time] 과 [state]의 곱 형태이다.
trace에 대해 저장을 하고 특정 time t 까지의 확률을 계산해서 저장한다.
Viterbi 알고리즘의 문젲점은 무엇이 있을까?
time step이 커지면 곱셈양이 증가한다. (확률곱) => 소수점이하로 떨어져서 0으로 인식한다. (underflow problem) => 그래서 log domain으로 계산을 한다.
Viterbi 알고리즘을 통해 𝜋, 𝑎, 𝑏, X 가 주어진 상황에서 training하고 새로 sequence가 들어오면 most probable assignment를 할수 있다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 10.1 Forward Sampling (0) | 2019.11.13 |
|---|---|
| Week 9.5 Baum-Welch Algorithm (0) | 2019.11.05 |
| Week 9.3 Forward-Backward probability Calculation (0) | 2019.10.17 |
| Week 9.2 Joint and Marginal Probability of HMM (0) | 2019.10.16 |
| Week 9.1 Concept of Hidden Markov Model (0) | 2019.10.15 |
