Hard margin 은 일체의 에러를 허용하지 않고 , Decision Boundary (DB)를 칼같이 나누는 경우를 말한다.
Soft margin은 반대로 어느정도 Error를 허용하고 DB를 나누는 경우이다.
Hard margin의 경우 Error를 대처 못할수 있다.
이것을 어떻게 처리할지에 대해 알아보자.
우선 Soft margin 에 대해 알아보자.

위의 그림에서 DB를 나누어 보는 방법은 아래의 3가지로 나눌수 있다.
1) 위의 보라색선 처럼 Non-linear 하게 나눌수 있거나,
2) 그래프 아래쪽의 파란색 점을 버리거나
3) DB에서 멀리 떨어진 거리만큼 패털티를 주고, 패널티 점수가 최소화 할수 있도록 하는 경우가 있다.
이번시간은 3)번의 경우에 대해 배워본다.

에러를 처리하는 2가지 방법에 대해 알아보자.
첫번째 , 0-1 Loss function 에 대해 알아본다.
DB의 법선 벡터 w는 quadratic programing 을 통해 만들었다.
기존 SVM 구하는 식에 에러의 갯수 * C (임의의 상수) 항을 추가하여 quadratic programing 에 넣어 볼수 있다.
Loss function 은 패널티를 어떻게 부가할지 정의하는 Function 이다.

위 그래프 x 축의 1지점은 (wxj+b)yj 가 파란색선 상에 파란점이 있는 부분이다. (위 슬라이드 1번 표시부분)
여기서 파란색 선은 Positive case 부분의 한계선이다.
에러가 없는 경우는 (wxj+b)yj 는 양의값을 가진다. DB에 가까워 질수록 이값은 줄어들고 파란색 라인에 오는 순간 1이 된다. 그리고 DB 라인을 지나는 경우에 error 가 발생하고 그때 1이라는 패널티를 부가하게 된다.
우리는 이것을 0-1 Loss function 이라 부른다.
하지만 0-1 Loss function 은 error 의 갯수가 quadratic programiing 을 통해 정확히 정의하기 어렵기 때문에 잘사용되지 않는다. 그리고 멀리있는 점이나 가까이 있는 점이나 동일한 패널티를 주기 때문에 공평한 패널티 부가라 할수 없다.
두번 째 , Hinge Loss function에 대해 알아보자. 이것은 많이 사용되는 모델이다.
파란색의 한계선까지는 0-1과 동일한 0의 패널티를 부가하고 한계선을 넘는순간 부터 패널티가 선형으로 증가하게된다 그리고 DB를 넘는순간은 1이 된다. 즉 DB에서 멀어질수록 더 많은 패널티를 부가한다.
이것은 slack variable을 통해 표현할수 있다.
slack variable은 miss clasification 되었을 때의 miss 되는 정도를 slack으로 두어 관리하겠다라는 의미이다.
C 는 slack variable의 얼마만큼의 강도로 설명할것인지 우리가 정해주는 parameter 이다.
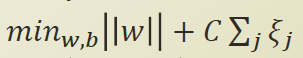
위 식은 slack을 모두 sum 해서 관리하고 최대한 minimum 되도록 노력하겠다는 의미이다.
그러면 Slack variable을 어떻게 정의할수 있냐?

Hard margin SVM 에서 front line이 1이라 가정하고 거기서 일부 j index(training instance)에서는 마이너스 slack이 발생할수 있겠다라고 표현할수 있고 , slack은 0과 같거나 그보다 크다. (0이면 에러가 없다.)
이렇게 정의된 Soft margin 의 문제는 무엇인가? 여전히 기존에 배운 quadratic programing을 통해 솔루션을 구할수 있지만 , C의 값을 우리가 정해야 하는 문제가 생긴다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 5.6. Rethinking of SVM (0) | 2019.07.20 |
|---|---|
| Week 5.5. Soft Margin with SVM (0) | 2019.07.19 |
| Week 5.2. Maximizing the Margin (0) | 2019.07.18 |
| Week 5.1. Decision Boundary with Margin (0) | 2019.07.17 |
| Week 4.8 Naive Bayes vs Logistic Regression (0) | 2019.07.17 |
