Week 8.3 강의를 통해 Lagrange Method를 통해 Multinomial distribution에서 MLE estimator를 찾아보았습니다.
이번시간에는 Multivariate Gaussian Distribution 를 배워보겠습니다.

MLE estimator를 찾기 위해 Log likelihood를 취하고 Optimize 해보면 된다. (미분해서 0이되는 값 찾는것)
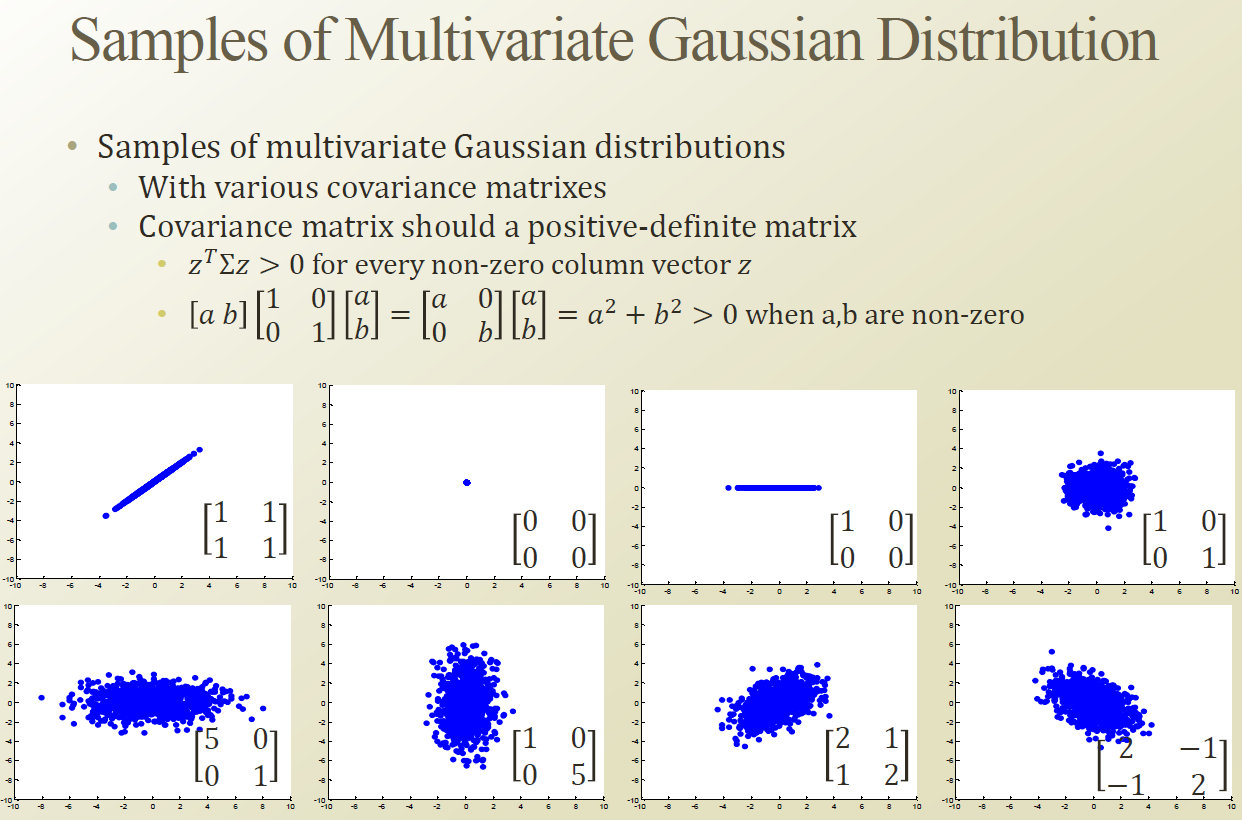
위의 그림의 왼쪽 위부터 하나씩 설명해 보자.
1) Variance : 1 , covariance : 1
2) 변화가 없으니 한포인트에 몰려있다.
3) 1로 선택된 한 dimension에 대해서만 분산이 존재하는 형태
4) 각 dimension 별로 variance 가 존재 , covariance 부분에서 분산이 없다는것 (= correlation과 매우 밀접한 연관이 있고 이부분이 0이라는 것이다. 즉 x y 의 연관성이 없기 때문에 원의 형태로 표현되었다.
5), 6) 특정 dimension이 좀더 높은 variance를 지니고 있고 covariance가 0라 타원의 형태이다.
7) Variance가 조금 있는데 (2) covariance이 (1)있다.
8) Variance가 조금 있는데 (2) covariance이 (-1)있다.
Mixture Model
Multinomial / Gaussian Distribution 2개를 연결하기 위해 Mixture Model 이 필요하다.
데이터 포인트를 관측해서 히스토그램을 그렸다고 하자. 봉우리가 3개가 있다.

이것이 Nomal로 fitting 이 될까? 아래의 빨간 그림인데 잘맞지 않다.
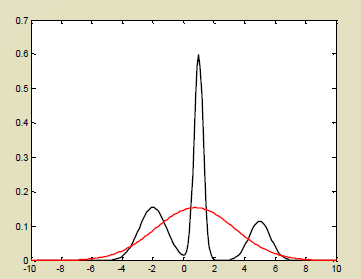
아래와 같이 근본이 다른 3개가 모인것이라 생각할수 있다.
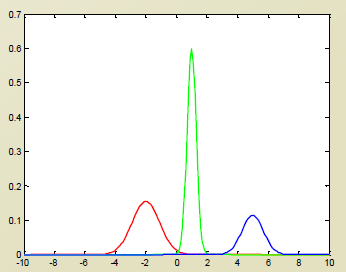
즉 이 히스토그램의 데이터는 Mixing 되어 하나의 데이터셋으로 받아들여 진것이라 생각하면된다.
(즉 Subpopulation 이 존재한다고 생각하면 된다.)

이것을 수학적으로 정의해보자.

πk 는 k의 선택지중에서 하나의 선택지를 선택할 확률이라 Multinomial Distribution을 쓸것이고 뒤의 N은 Multivariate Gaussian Distribution 을 쓰겠다는 의미이다.
즉 Multivariate Gaussian Distribution 부분은 k개의 Nomal 이라하고 subpopulation 에 대해 fitting 된 distribution 이다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 8.7 Relation between K-means and GMM (0) | 2019.10.09 |
|---|---|
| Week 8.5 Gaussian Mixture Model (0) | 2019.10.07 |
| Week 8.3 Multinomial Distribution (0) | 2019.10.03 |
| Week 8.2 K-Means Algorithm 2 (0) | 2019.10.01 |
| Week 8.1 K-Means Algorithm 1 (0) | 2019.09.30 |
