Ridge Regression , Lasso Regression 의 예제를 살펴보자.
먼저 Ridge Regression 을 이용한 Linear regression 을 해보자.
Linear 이기 때문에 Xw 로 두고 w에 대해 편미분을 해보자.

λ(람다)는 우리가 결정하는 값이다. Linear Regression 과 다른점은 λI 의 term이 추가되었다.
그러면 Regularization 을 했을 때 와 안했을 때를 살펴 보자.
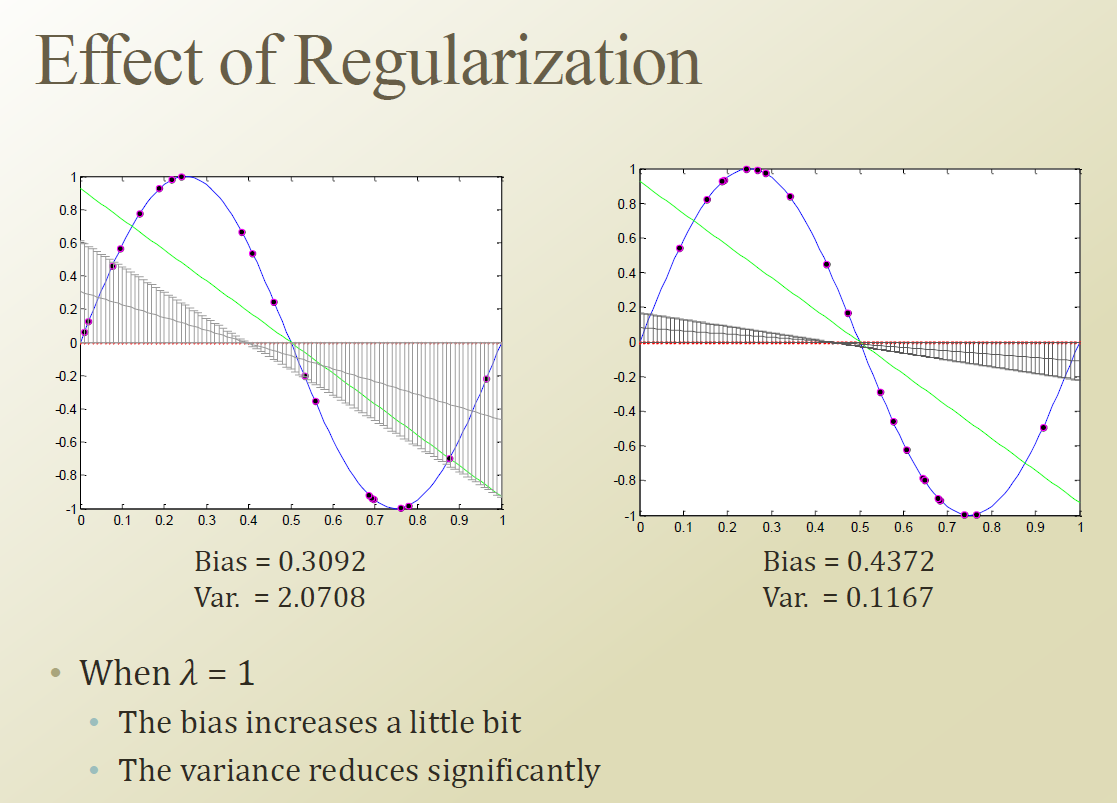
왼쪽 그래프가 Regularization 을 안한 경우이다.
오른쪽의 Regularizaiton 을 한경우는 동일한 데이터셋에 대해서 Variance가 줄어드는것을 알수 있다. 좀 덜 민감하게 반응한다. 하지만 모델의 complexity는 바뀌지 않았다. Bias는 살짝 증가했다. Perfect fit을 하지 않겠다는 제약조건때문에 증가한것이다. Variance는 크게 줄어 전체적인 에러값은 줄어듬을 알수 있다.

λ(람다) 가 크면 Regularization term 이 커지기 때문에 에러를 줄어들게 하려는 노력이 상쇄 되어 버려 , 모델의 complexity 가 줄어들게 된다.
그러면 적정한 수준의 λ(람다)값은 어떻게 찾아야 하나? 실험을 여러번 해봐야 알수 있다.

Logistic regression 은 CLosed form solution으로 떨어지지 않고 , Approximation 해야 되는 부분이 필요하다.

C term 이 Regularization 과 유사한 역할을 하는 term 이다. C를 조절하면서 DB가 어떻게 변하는지를 볼수 있었다.
즉 SVM은 soft margin을 감안한 순간에 이미 Regularizaiton 을 고려한 것이다.
'머신러닝 > 문일철 교수님 강의 정리 (인공지능및기계학습개론)' 카테고리의 다른 글
| Week 8.1 K-Means Algorithm 1 (0) | 2019.09.30 |
|---|---|
| Week 7.9 Simple Example of Belief Propagation (0) | 2019.09.26 |
| Week 6.6 Definition of Regularization (0) | 2019.08.19 |
| Week 6.5. Performance Metrics (0) | 2019.08.18 |
| Weeek 6.4 Cross Validation (0) | 2019.08.17 |
